Mais passeios aleatórios

Na última publicação, analisamos um problema de passeios aleatórios, que podemos traduzir nesta figura

Distância ao nó 6 (passeio aleatório)

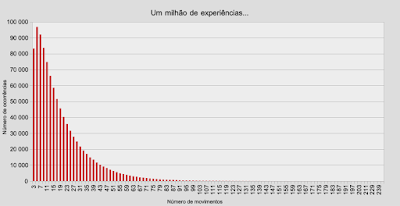
em que temos um grafo com 6 nós e as distâncias que um viajante aleatório colocado num dos outros nós teria de percorrer em média para chegar ao nó 6.

Estes números costumam causar um certo desconforto, por chocarem com a nossa intuição, mas não deixam de ser verdade...

E se os seis nós estivessem em linha? As equações seriam

6 nós em linha

T5 = [1 + (1 + T4)] / 2

T4 = [(1 + T5) + (1 + T3)] / 2

T3 = [(1 + T4) + (1 + T2)] / 2

T2 = [(1 + T3) + (1 + T1)] / 2

T1 = 1 + T2

e eliminado sucessivamente T1, T2, T3 e T4

T2 = [(1 + T3) + (1 + 1 + T2)] / 2

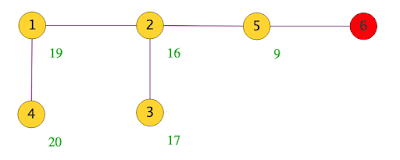
T2 = 3 + T3

T3 = [(1 + T4) + (1 + 3 + T3)] / 2

T3 = 5 + T4

T4 = [(1 + T5) + (1 + 5 + T4)] / 2

T4 = 7 + T5

T5 = [1 + (1 + 7 + T5)] / 2

T5 = 9

e daqui que todas as distâncias que teriam de ser percorridas em média por um viajante colocado num nó de partida qualquer para chegar ao nó 6 serão as indicadas na figura a seguir

Distância ao nó 6 (passeio aleatório)

E se tivermos uma fila com N nós? Que distância teria de percorrer em média um viajante aleatório para vencer essa distância? Será (N - 1)^2?

Outra questão diferente será saber quantas vezes o viajante passou por cada nó, em média. No layout de um museu, ou de um espaço comercial, onde as pessoas se movam com alguma aleatoriedade, esse valor pode ser uma medida da qualidade da sua localização.

Fica o desafio.

Passeios aleatórios

Este problema pode ser apresentado sob as mais diversas formas.

Imaginemos um edifício com seis salas, e que um visitante, que está na sala 1, se move aleatoriamente entre as salas, com a probabilidade de escolher uma porta igual para todas as portas da sala.

Organização das salas

A questão é quantos movimentos terá de fazer, em média, o visitante até chegar à sala 6?

Ou poderia ser, quantos movimentos terá de fazer, em média, antes de visitar todas as salas?

Também podemos olhar para este problema, por exemplo, como um grafo

Grafo equivalente

e utilizar conceitos de teoria dos grafos.

E pensar que os nós poderiam ser páginas na Web e as ligações poderiam ser os links entre elas, e o problema ser qual é a página mais visitada por um viajante aleatório na Web.

Estes processos em que o caminhante decide aleatoriamente cada movimento não têm memória, cada decisão é independente do histórico anterior, é uma cadeia de Markov.

Quando está no nó 5, por exemplo, o caminhante tem duas alternativas igualmente prováveis, ir para o nó 6 e terminar ou então regressar ao nó 2, a partir do qual terá de realizar T2 movimentos para chegar ao nó 6. Assim, em média, para ir de 5 a 6 precisamos dos seguintes movimentos

T5 = [1 + (1 + T2)] / 2 

Da mesma maneira, podemos dizer que 

T2 = [(1 + T1) + (1 + T3) + (1 + T5)] / 3

T3 = 1 + T2

T1 = [(1 + T2) + (1 + T4)] / 2

T4 = 1 + T1.

Isto agora é álgebra, resolução de sistemas, em que estamos interessados apenas em T1.

Eliminando T4 na penúltima equação, ficamos com um equação em T1 e T2

T1 = [(1 + T2) + (2 + T1)] / 2.

Eliminando T3 na segunda equação, ficamos com

T2 = [(1 + T1) + (2 + T2) + (1 + T5) ] / 3.

Eliminando T5 nesta, ficamos com uma segunda equação em T1 e T2

T2 = [(1 + T1) + (2 + T2) + (1 + [1 + (1 + T2)] / 2)] / 3.

Da primeira destas duas equações retiramos

2T1 = 1 + T2 + 2 + T1

T2 = T1 - 3

e substituindo na última

6T1 - 18 = 2 + 2T1 + 4 + 2T1 - 6 + 2 + 1 + 1 + T1 - 3

T1 = 19.

Em média, são necessários 19 movimentos, um número talvez surpreendentemente elevado!...

Fizemos uma simulação de 1 milhão de passeios aleatórios, usando um programa de computador muito simples, que confirmou estes resultados: média 19 e moda 5.

Fica aqui o gráfico da distribuição dos comprimentos desse milhão de percursos, todos evidentemente de comprimento ímpar...

Histograma da distribuição de comprimentos

E assim se conjugam alguns saberes para se encontrar a solução de um problema aparentemente simples mas muito desafiante, e que permite encontrar outros, e novos, desafios...