Genealogia: Primeiros Passos

Já nem me lembro quando exactamente comecei a dar os primeiros passos nesta actividade de registar e partilhar quem são os meus antepassados. Apenas sei que nunca usei papeis, folhas de cálculo, ou outros suportes pessoais, e que, desde o primeiro dia, aderi ao uso de plataformas na Web, e ainda bem que o fiz.

Os nossos antepassados não são só nossos, e se é certo que temos dois pais, quatro avós, oito bisavós, etc, um nosso antepassado pode ter centenas ou milhares de descendentes, e nada mais interessante que descobrirmos outros descendentes dos nossos avoengos e com eles partilharmos as nossas descobertas.

Em Portugal, os registos civis de nascimento, casamento e óbito iniciaram-se com a implantação da república, e, até lá, havia apenas os registos paroquiais, que se iniciaram no final do século XVI, e que agora estão à guarda dos arquivos distritais.
Há um assinalável esforço de digitalização deste enorme acervo por parte dos arquivos distritais, e hoje é possível aceder via Internet à maioria destes registos. Há muitas formas de lá chegar, mas sem dúvida que a mais prática será pela página tombo.pt, mantida por João Ventura, e que fornece apontadores para todos esses arquivos, ano a ano, distrito a distrito, concelho a concelho e freguesia a freguesia.
São milhões de páginas, algumas de fácil leitura e outras não, dependendo do estado de conservação e da letra de quem as escreveu, do uso da época, etc, mas todo um mundo de informações históricas, que vai bastante além dos simples registos familiares.
Para além dos arquivos da igreja Católica, há os registos de muitas instituições, os arquivos familiares das casas mais importantes, livros, crónicas, e uma infinidade de documentos que também estão a ser continuamente digitalizados e disponibilizados.

Primeiros passos

Alguém me falou no MyHeritage, há talvez uma dezena de anos, e decidi registar-me e começar a introduzir os dados que fui recolhendo nesta plataforma, começando pelos vivos e depois pelos já falecidos, começando pelos mais recentes.
Na altura, uma conta gratuita estava limitada a 250 pessoas, e rapidamente cheguei e esse limite, mas nunca coloquei a hipótese de ter de pagar para disponibilizar a outros os dados que recolhia com o meu trabalho.
Entretanto, já conhecia outras plataformas, e já me tinha registado no Ancestry. Também tinha ouvido falar no formato GEDCOM de importação/exportação de árvores genealógicas, e usei-o para exportar com exito a minha árvore inicial do MyHeritage para o Ancestry, que é, desde então, a plataforma onde guardo a minha árvore oficial, com todos os documentos comprovativos, fotografias, etc.
Entretanto, tudo evoluiu, desde a capacidade das plataformas até aos conceitos de colaboração e partilha, e hoje estas plataformas oferecem uma capacidade ilimitada de armazenamento de dados, cobrando apenas por alguns serviços de pesquisa.
Uma outra plataforma, Geneanet, tem igualmente tido muito sucesso, e também mantenho a minha árvore actualizada nessa plataforma, para beneficiar das sugestões que me são oferecidas.

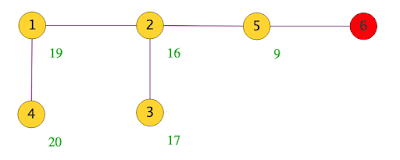
Mapa elaborado pelo Geneanet

FamilySearch

Hoje, FamilySearch, um projecto da Igreja de Jesus Cristo dos Santos dos Últimos Dias, é absolutamente incontornável na pesquisa dos nossos antepassados.

Digitalizar e indexar todos os documentos disponíveis em todos os países no mundo, construir uma árvore genealógica mundial, e associar os documentos indexados a pessoas reais, vivas ou falecidas, de uma forma colaborativa, por milhões de pessoas, a maior parte das quais nem sequer compreende esta natureza colaborativa do projecto e toma por verdadeiras todas as sugestões que lhes são propostas, é um projecto gigantesco.

Continuarei esta história em próximos textos.

Outras notas de minha autoria

i) Francisco Restivo, Genealogia, em Aqui há Informática
ii) Francisco Restivo, Genealogia: FamilySearch, em Aqui há Informática
iii) Francisco Restivo, Visualizing family networks, em Medium.

Genealogia: FamilySearch

Atrevo-me a dar continuidade a uma entrada anterior sobre Genealogia, tecendo algumas considerações sobre o projecto FamilySearch.org, pela sua relevância como projecto na área da Informática, da informação automática, de enorme ambição, e colaborativo, e portanto exposto às naturais incompreensões de muitos que o usam e que idealizam capacidades factualmente inatingíveis.

O FamilySearch tem como objectivo chegar a uma árvore genealógica única, universal, partilhada entre todos os utilizadores, uns mais, outros menos cuidadosos, baseada em pessoas, documentos, e relações entre pessoas e entre pessoas e documentos, utilizando o trabalhos de voluntários, a indexação automática, e as pessoas e as anexações entre pessoas e documentos que os utilizadores vão acrescentando ao sistema. 

Um utilizador registado (é gratuito) começa por criar a sua própria árvore familiar, acrescentando familiares ou manualmente ou através de um ficheiro GEDCOM, sendo certo que a plataforma vai alertando para possíveis repetições, já que, obviamente, uma pessoa pode pertencer a múltiplas árvores familiares. Se o utilizador confirmar a coincidência proposta, as duas árvores familiares em causa são fundidas, e as famílias alargadas.

Cada pessoa tem uma ficha com os seus dados vitais, onde todas as alterações são anotadas

Dados vitais do meu bisavô João.

Os documentos nos arquivos, nomeadamente os assentos de baptismo, casamento, e óbito, são escritos por pessoas, com a letra da época, umas vezes cheios de pressa, outras não, com os nomes dos envolvidos, a que se pode acrescentar a sua localização (data, livro, página, etc).

Assento de baptismo do meu bisavô (João da Costa, digo) João, filho legítimo de José dos Santos e Maria Rita de Sousa, da aldeia de Pinheiro d'Aquem, desta freguesia de São Veríssimo de Valbom, nasceu aos vinte e seis de Novembro de mil oitocentos e quatorze anos...

A leitura automática ou manual que o FamilySearch faz/fez é muito sujeita a erros, decorrentes da letra, do estado de conservação, da experiência de quem lê, mas é sempre possível comunicar os erros.

Estes documentos podem ser anexados a pessoas (o próprio, pais, conjuge, avós paternos e maternos, etc, conforme a época e o uso), e essa tarefa é da responsabilidade dos utilizadores.

Quando se faz uma pesquisa, é-nos devolvida uma lista normalmente muito extensa de possibilidades, ordenadas por ordem decrescente da probabilidade de serem de interesse, com a indicação se é possível a visualização da fonte e/ou se estão já associadas a alguma pessoa, em alguma árvore.

Exemplo do resultado de uma pesquisa

O grande problema resulta do facto de a maior parte dos documentos paroquiais não serem disponibilizados, devido às restrições impostas pelo estado português, e ser necessária alguma imaginação para se chegar aos documentos originais, recorrendo, por exemplo, aos apontadores disponibilizados em tombo.pt.

Pessoalmente, mantenho a minha árvore genealógica noutra plataforma, no meu caso Ancestry.com,  à qual anexo todos os documentos que consigo identificar, e, neste aspecto, o FamilySearch é uma grande ajuda.

Genealogia

Descobrir as raízes, organizar a informação relativa aos nossos antepassados, tem fortes relações com a Informática.
Cada um organiza a sua pesquisa genealógica como entende, e há muitas alternativas hoje, cada uma com as suas vantagens e inconvenientes.
Eu sempre usei uma plataforma online gratuita para guardar a minha árvore, comecei pelo MyHeritage, e, quando atingi os primeiros 500 membros, porque na altura deixava de ser gratuita, passei para o Ancestry.
Apesar dessa limitação ter desaparecido, hoje continuo a usar o Ancestry, e anexo a cada pessoa da árvore os registos paroquiais respectivos, outros documentos, e mesmo fotos.

Raiz da minha árvore genealógica no Ancestry

Realmente, mantenho cópias da minha árvore noutras plataformas, desde logo no MyHeritage e no Geneanet, tirando partido do facto de haver um formato de ficheiro genealógico GEDCOM compatível com estas plataformas, e não só.
Como estas plataformas enviam aos utilizadores muitas sugestões de familiares, algumas certas, outras erradas, embora quase todas acessíveis através de um registo pago, que eu nunca fiz, há sempre uma pista ou outra que se pode aproveitar.
E também todas permitem imprimir a nossa árvore em diversos formatos, como esta, retirada do Geneanet

Árvore importada do Geneanet.org (5 gerações)

Comecei por pesquisar directamente nos registos paroquiais online.
Os registos paroquiais até 1910, ou um pouco mais, excepto os que se extraviaram, estão guardados nos Arquivos Distritais e acessiveis através das suas plataformas, ou então usando o indispensável Tombo.pt, que disponibiliza links para todos os livros, e muitos mais documentos, e mesmo uma extensão para o Chrome, uma ferramenta de leitura dos livros paroquiais com muita utilidade.

Outra plataforma indispensável é o blogue GenealogiaFB.
Sendo a genealogia uma actividade colaborativa, pela simples razão de o mesmo antepassado poder pertencer a múltiplas árvores, e ser desafiante saber o que outros descobriram sobre esse antepassado nosso, neste momento rendi-me ao FamilySearch como instrumento de pesquisa.
O FamilySearch basicamente digitalizou a maior parte dos registos disponíveis em todo o mundo, indexou-os automaticamente, com os erros inerentes à leitura automática de manuscritos muitas vezes quase indecifráveis, e permite associá-los a pessoas.
Tem o conceito de árvore genealógica única, construída através da junção das contribuições de todos, e sempre que acrescentamos uma pessoa à nossa árvore ele tenta saber se essa pessoa por acaso já estará nessa árvore gigante ou não, procurando evitar duplicações.
Todas as acções ou correcções ficam registadas.
É uma ferramenta bastante mais complexa que as anteriores, mas em que, na minha opinião, vale a pena investir tempo.
Finalmente, visito muitas vezes o forum de genealogia Geneall, para procurar interessados nas minhas investigações.

[uma continuação aqui]

Manobras com baldes

Propuseram-me recentemente este conhecido problema:

dados três baldes, um cheio com oito litros de água, e dois vazios, um com cinco litros e outro com três litros de capacidade, todos sem graduação, descobrir a forma de passar quatro litros de água do primeiro para o segundo balde, com o número mínimo de movimentos:

Não gosto de métodos empíricos, pelo que explorei a hipótese de transformar este problema num problema de determinação do caminho mínimo entre dois vértices de um grafo. Um grafo tem vértices e arestas. Os vértices seriam os estados inicial, intermédios e final, e as arestas indicariam ser possível transitar de um para outro estado com um movimento.

Primeira questão, de quantas formas será possível distribuir os 8 litros de água pelos três baldes, necessariamente um número inteiro de litros em cada balde. Bem, seria possível usar aqui a regra dos separadores para este cálculo, mas a resposta está à distância de um pequeno programa de computador:

São 24! Faltando saber se são todos estados possíveis dentro das regras definidas.

Em cada estado há no máximo 6 movimentos possíveis, do balde 1 para os baldes 2 ou 3, do balde 2 para os baldes 1 ou 3, e do balde 3 para os baldes 1 ou 2, desde que o balde de partida tenha água, e o movimento pode consistir em despejar a água toda ou em encher o balde de destino, não havendo situações intermédias, uma vez que os baldes não têm graduações.

Quantas arestas terá este grafo? Outro pequeno programa de computador ajuda a descobrir que são 106:

e o problema estará resolvido!

O próximo passo é visualizar este grafo (direccionado, digrafo). Utilizei Gephi:

Curiosamente, há 8 vértices inatingíveis (bons para problemas impossíveis...). Retirando-os, e pedindo ao Gephi que mostre, se houver, o caminho mais curto entre os vértices [8, 0, 0] e [4, 4, 0], chegamos a uma solução com comprimento 7 (ramo superior):

Há também uma solução óbvia com comprimento 8 (ramo inferior) e mais um conjunto de soluções de maior comprimento, passando todas pelo vértice [0, 5, 3].

Mais passeios aleatórios

Na última publicação, analisamos um problema de passeios aleatórios, que podemos traduzir nesta figura

Distância ao nó 6 (passeio aleatório)

em que temos um grafo com 6 nós e as distâncias que um viajante aleatório colocado num dos outros nós teria de percorrer em média para chegar ao nó 6.

Estes números costumam causar um certo desconforto, por chocarem com a nossa intuição, mas não deixam de ser verdade...

E se os seis nós estivessem em linha? As equações seriam

6 nós em linha

T5 = [1 + (1 + T4)] / 2

T4 = [(1 + T5) + (1 + T3)] / 2

T3 = [(1 + T4) + (1 + T2)] / 2

T2 = [(1 + T3) + (1 + T1)] / 2

T1 = 1 + T2

e eliminado sucessivamente T1, T2, T3 e T4

T2 = [(1 + T3) + (1 + 1 + T2)] / 2

T2 = 3 + T3

T3 = [(1 + T4) + (1 + 3 + T3)] / 2

T3 = 5 + T4

T4 = [(1 + T5) + (1 + 5 + T4)] / 2

T4 = 7 + T5

T5 = [1 + (1 + 7 + T5)] / 2

T5 = 9

e daqui que todas as distâncias que teriam de ser percorridas em média por um viajante colocado num nó de partida qualquer para chegar ao nó 6 serão as indicadas na figura a seguir

Distância ao nó 6 (passeio aleatório)

E se tivermos uma fila com N nós? Que distância teria de percorrer em média um viajante aleatório para vencer essa distância? Será (N - 1)^2?

Outra questão diferente será saber quantas vezes o viajante passou por cada nó, em média. No layout de um museu, ou de um espaço comercial, onde as pessoas se movam com alguma aleatoriedade, esse valor pode ser uma medida da qualidade da sua localização.

Fica o desafio.

Passeios aleatórios

Este problema pode ser apresentado sob as mais diversas formas.

Imaginemos um edifício com seis salas, e que um visitante, que está na sala 1, se move aleatoriamente entre as salas, com a probabilidade de escolher uma porta igual para todas as portas da sala.

Organização das salas

A questão é quantos movimentos terá de fazer, em média, o visitante até chegar à sala 6?

Ou poderia ser, quantos movimentos terá de fazer, em média, antes de visitar todas as salas?

Também podemos olhar para este problema, por exemplo, como um grafo

Grafo equivalente

e utilizar conceitos de teoria dos grafos.

E pensar que os nós poderiam ser páginas na Web e as ligações poderiam ser os links entre elas, e o problema ser qual é a página mais visitada por um viajante aleatório na Web.

Estes processos em que o caminhante decide aleatoriamente cada movimento não têm memória, cada decisão é independente do histórico anterior, é uma cadeia de Markov.

Quando está no nó 5, por exemplo, o caminhante tem duas alternativas igualmente prováveis, ir para o nó 6 e terminar ou então regressar ao nó 2, a partir do qual terá de realizar T2 movimentos para chegar ao nó 6. Assim, em média, para ir de 5 a 6 precisamos dos seguintes movimentos

T5 = [1 + (1 + T2)] / 2 

Da mesma maneira, podemos dizer que 

T2 = [(1 + T1) + (1 + T3) + (1 + T5)] / 3

T3 = 1 + T2

T1 = [(1 + T2) + (1 + T4)] / 2

T4 = 1 + T1.

Isto agora é álgebra, resolução de sistemas, em que estamos interessados apenas em T1.

Eliminando T4 na penúltima equação, ficamos com um equação em T1 e T2

T1 = [(1 + T2) + (2 + T1)] / 2.

Eliminando T3 na segunda equação, ficamos com

T2 = [(1 + T1) + (2 + T2) + (1 + T5) ] / 3.

Eliminando T5 nesta, ficamos com uma segunda equação em T1 e T2

T2 = [(1 + T1) + (2 + T2) + (1 + [1 + (1 + T2)] / 2)] / 3.

Da primeira destas duas equações retiramos

2T1 = 1 + T2 + 2 + T1

T2 = T1 - 3

e substituindo na última

6T1 - 18 = 2 + 2T1 + 4 + 2T1 - 6 + 2 + 1 + 1 + T1 - 3

T1 = 19.

Em média, são necessários 19 movimentos, um número talvez surpreendentemente elevado!...

Fizemos uma simulação de 1 milhão de passeios aleatórios, usando um programa de computador muito simples, que confirmou estes resultados: média 19 e moda 5.

Fica aqui o gráfico da distribuição dos comprimentos desse milhão de percursos, todos evidentemente de comprimento ímpar...

Histograma da distribuição de comprimentos

E assim se conjugam alguns saberes para se encontrar a solução de um problema aparentemente simples mas muito desafiante, e que permite encontrar outros, e novos, desafios...

Ciência de Dados

Os computadores, como todas as máquinas, são produtos da mente humana, e terão como última utilidade aliviar os humanos de tarefas em que os podem substituir com vantagem, esperando-se que daí resulte uma vida mais feliz, mais tempo livre, e uma sociedade mais inteligente.

Talvez por isso, saber como funciona um computador, saber configurar ou manter em funcionamento um parque de máquinas, mesmo saber programá-las, é útil, mas fica muito longe de contribuir para responder aos desafios que nos são colocados.

No mundo de hoje, as competências digitais não são simples competências para programar, ou para lidar com as tecnologias. São competências para pensar e planear para um mundo digital, para analisar problemas e formular soluções que possam ser executadas automaticamente por uma máquina de processamento de informação.
Ao desafios de lidar com as tecnologias, soma-se agora a necessidade de compreender como funciona o mundo global, a economia do conhecimento, as redes, a propagação de ideias, o contágio, a influência, e as decisões que afectam as nossas vidas.

Neste mundo de dados, saber onde os encontrar, saber extrair informação, saber formular questões baseadas em dados, saber obter as respostas, são competências essenciais em todas as áreas científicas, e nomeadamente nas ciências sociais e humanas, aquelas que estudam os nossos comportamentos individuais e colectivos.

Estamos a falar de Ciência de Dados, uma área que está a crescer em todo o mundo e também em Portugal, onde já são várias as Universidades que oferecem Licenciaturas e Mestrados, e uma área apetecível, para o bem e para o mal... todos nos lembramos da utilização de dados das redes sociais para interferir em eleições, do crédito social dos chineses, ou da ameaça de monitorização do pensamento de cada um...

De qualquer modo, como sempre na vida, a ignorância é o maior perigo...