Manobras com baldes

Propuseram-me recentemente este conhecido problema:

dados três baldes, um cheio com oito litros de água, e dois vazios, um com cinco litros e outro com três litros de capacidade, todos sem graduação, descobrir a forma de passar quatro litros de água do primeiro para o segundo balde, com o número mínimo de movimentos:

Não gosto de métodos empíricos, pelo que explorei a hipótese de transformar este problema num problema de determinação do caminho mínimo entre dois vértices de um grafo. Um grafo tem vértices e arestas. Os vértices seriam os estados inicial, intermédios e final, e as arestas indicariam ser possível transitar de um para outro estado com um movimento.

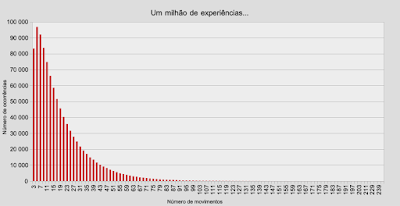
Primeira questão, de quantas formas será possível distribuir os 8 litros de água pelos três baldes, necessariamente um número inteiro de litros em cada balde. Bem, seria possível usar aqui a regra dos separadores para este cálculo, mas a resposta está à distância de um pequeno programa de computador:

São 24! Faltando saber se são todos estados possíveis dentro das regras definidas.

Em cada estado há no máximo 6 movimentos possíveis, do balde 1 para os baldes 2 ou 3, do balde 2 para os baldes 1 ou 3, e do balde 3 para os baldes 1 ou 2, desde que o balde de partida tenha água, e o movimento pode consistir em despejar a água toda ou em encher o balde de destino, não havendo situações intermédias, uma vez que os baldes não têm graduações.

Quantas arestas terá este grafo? Outro pequeno programa de computador ajuda a descobrir que são 106:

e o problema estará resolvido!

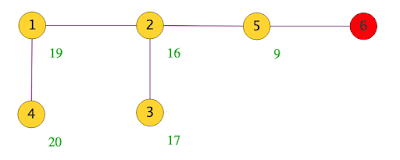
O próximo passo é visualizar este grafo (direccionado, digrafo). Utilizei Gephi:

Curiosamente, há 8 vértices inatingíveis (bons para problemas impossíveis...). Retirando-os, e pedindo ao Gephi que mostre, se houver, o caminho mais curto entre os vértices [8, 0, 0] e [4, 4, 0], chegamos a uma solução com comprimento 7 (ramo superior):

Há também uma solução óbvia com comprimento 8 (ramo inferior) e mais um conjunto de soluções de maior comprimento, passando todas pelo vértice [0, 5, 3].

Mais passeios aleatórios

Na última publicação, analisamos um problema de passeios aleatórios, que podemos traduzir nesta figura

Distância ao nó 6 (passeio aleatório)

em que temos um grafo com 6 nós e as distâncias que um viajante aleatório colocado num dos outros nós teria de percorrer em média para chegar ao nó 6.

Estes números costumam causar um certo desconforto, por chocarem com a nossa intuição, mas não deixam de ser verdade...

E se os seis nós estivessem em linha? As equações seriam

6 nós em linha

T5 = [1 + (1 + T4)] / 2

T4 = [(1 + T5) + (1 + T3)] / 2

T3 = [(1 + T4) + (1 + T2)] / 2

T2 = [(1 + T3) + (1 + T1)] / 2

T1 = 1 + T2

e eliminado sucessivamente T1, T2, T3 e T4

T2 = [(1 + T3) + (1 + 1 + T2)] / 2

T2 = 3 + T3

T3 = [(1 + T4) + (1 + 3 + T3)] / 2

T3 = 5 + T4

T4 = [(1 + T5) + (1 + 5 + T4)] / 2

T4 = 7 + T5

T5 = [1 + (1 + 7 + T5)] / 2

T5 = 9

e daqui que todas as distâncias que teriam de ser percorridas em média por um viajante colocado num nó de partida qualquer para chegar ao nó 6 serão as indicadas na figura a seguir

Distância ao nó 6 (passeio aleatório)

E se tivermos uma fila com N nós? Que distância teria de percorrer em média um viajante aleatório para vencer essa distância? Será (N - 1)^2?

Outra questão diferente será saber quantas vezes o viajante passou por cada nó, em média. No layout de um museu, ou de um espaço comercial, onde as pessoas se movam com alguma aleatoriedade, esse valor pode ser uma medida da qualidade da sua localização.

Fica o desafio.

Passeios aleatórios

Este problema pode ser apresentado sob as mais diversas formas.

Imaginemos um edifício com seis salas, e que um visitante, que está na sala 1, se move aleatoriamente entre as salas, com a probabilidade de escolher uma porta igual para todas as portas da sala.

Organização das salas

A questão é quantos movimentos terá de fazer, em média, o visitante até chegar à sala 6?

Ou poderia ser, quantos movimentos terá de fazer, em média, antes de visitar todas as salas?

Também podemos olhar para este problema, por exemplo, como um grafo

Grafo equivalente

e utilizar conceitos de teoria dos grafos.

E pensar que os nós poderiam ser páginas na Web e as ligações poderiam ser os links entre elas, e o problema ser qual é a página mais visitada por um viajante aleatório na Web.

Estes processos em que o caminhante decide aleatoriamente cada movimento não têm memória, cada decisão é independente do histórico anterior, é uma cadeia de Markov.

Quando está no nó 5, por exemplo, o caminhante tem duas alternativas igualmente prováveis, ir para o nó 6 e terminar ou então regressar ao nó 2, a partir do qual terá de realizar T2 movimentos para chegar ao nó 6. Assim, em média, para ir de 5 a 6 precisamos dos seguintes movimentos

T5 = [1 + (1 + T2)] / 2 

Da mesma maneira, podemos dizer que 

T2 = [(1 + T1) + (1 + T3) + (1 + T5)] / 3

T3 = 1 + T2

T1 = [(1 + T2) + (1 + T4)] / 2

T4 = 1 + T1.

Isto agora é álgebra, resolução de sistemas, em que estamos interessados apenas em T1.

Eliminando T4 na penúltima equação, ficamos com um equação em T1 e T2

T1 = [(1 + T2) + (2 + T1)] / 2.

Eliminando T3 na segunda equação, ficamos com

T2 = [(1 + T1) + (2 + T2) + (1 + T5) ] / 3.

Eliminando T5 nesta, ficamos com uma segunda equação em T1 e T2

T2 = [(1 + T1) + (2 + T2) + (1 + [1 + (1 + T2)] / 2)] / 3.

Da primeira destas duas equações retiramos

2T1 = 1 + T2 + 2 + T1

T2 = T1 - 3

e substituindo na última

6T1 - 18 = 2 + 2T1 + 4 + 2T1 - 6 + 2 + 1 + 1 + T1 - 3

T1 = 19.

Em média, são necessários 19 movimentos, um número talvez surpreendentemente elevado!...

Fizemos uma simulação de 1 milhão de passeios aleatórios, usando um programa de computador muito simples, que confirmou estes resultados: média 19 e moda 5.

Fica aqui o gráfico da distribuição dos comprimentos desse milhão de percursos, todos evidentemente de comprimento ímpar...

Histograma da distribuição de comprimentos

E assim se conjugam alguns saberes para se encontrar a solução de um problema aparentemente simples mas muito desafiante, e que permite encontrar outros, e novos, desafios...

Ciência de Dados

Os computadores, como todas as máquinas, são produtos da mente humana, e terão como última utilidade aliviar os humanos de tarefas em que os podem substituir com vantagem, esperando-se que daí resulte uma vida mais feliz, mais tempo livre, e uma sociedade mais inteligente.

Talvez por isso, saber como funciona um computador, saber configurar ou manter em funcionamento um parque de máquinas, mesmo saber programá-las, é útil, mas fica muito longe de contribuir para responder aos desafios que nos são colocados.

No mundo de hoje, as competências digitais não são simples competências para programar, ou para lidar com as tecnologias. São competências para pensar e planear para um mundo digital, para analisar problemas e formular soluções que possam ser executadas automaticamente por uma máquina de processamento de informação.
Ao desafios de lidar com as tecnologias, soma-se agora a necessidade de compreender como funciona o mundo global, a economia do conhecimento, as redes, a propagação de ideias, o contágio, a influência, e as decisões que afectam as nossas vidas.

Neste mundo de dados, saber onde os encontrar, saber extrair informação, saber formular questões baseadas em dados, saber obter as respostas, são competências essenciais em todas as áreas científicas, e nomeadamente nas ciências sociais e humanas, aquelas que estudam os nossos comportamentos individuais e colectivos.

Estamos a falar de Ciência de Dados, uma área que está a crescer em todo o mundo e também em Portugal, onde já são várias as Universidades que oferecem Licenciaturas e Mestrados, e uma área apetecível, para o bem e para o mal... todos nos lembramos da utilização de dados das redes sociais para interferir em eleições, do crédito social dos chineses, ou da ameaça de monitorização do pensamento de cada um...

De qualquer modo, como sempre na vida, a ignorância é o maior perigo...

Fourier e a pandemia

Decidi investigar se, nos vários países, haveria uma periodicidade semanal na sequência de casos CoVid-19 registados diariamente.
Usei os dados fornecidos pela John Hopkins University, e fiz um pequeno programa que, para um país escolhido, retira a sequência de resultados disponíveis (casos acumulados), constrói a sequência de casos dia a dia, calcula a transformada de Fourier desta sequência, e mostra os resultados.
Por exemplo, para Portugal obtive (deixemos de lado a escala...)

Visível a sequência de casos diários conhecida (a azul) e, a laranja, a transformada de Fourier dessa sequência. A outra metade seria simétrica desta. Aquele pico por volta do índice 20 corresponde à periodicidade semanal! Et voilà!
Realmente, sendo a frequência de amostragem 1 por dia, e 145 o número de amostras, a frequência 1 em cada 7 dias estará no índice 145/7.
Curiosamente, noutros países encontrei picos mais nítidos, como na Alemanha

e mesmo na Itália

que interpreto como um funcionamento menos caótico do sistema de registo dos dados...
Será?

Modelos matemáticos e contágios

Numa população, um elemento infectado pode provocar uma epidemia, ou não.
Se o contágio se fizer por contacto físico (social), os principais parâmetros a considerar serão o número de contactos (por dia) e a probabilidade de um contacto provocar um contágio.
Outros parâmetros importantes, serão o tempo da infecção, percentagem de casos letais, e se os sobreviventes ficam vacinados, ou não.
Numa população que se distribui de uma forma não uniforme, em comunidades com hábitos sociais variados, com distribuição geográfica variada, com dados de fiabilidade não comprovada, sugere um grande desafio de modelação e de previsão.
Num grupo uniforme, se, por exemplo, um infectado provocar 2 contágios por dia, aparentemente teremos um crescimento exponencial 1-2-4-8-16-32-64-128-... Será assim? Não parece.
O modelo exponencial só é válido numa população infinita, ou então, em grupos uniformes e enquanto o contágio não atinja valores significativos.
Nesta figura, o ajuste de uma curva exponencial a um caso real, a pandemia Coronavírus em Portugal na data de hoje: (ver código aqui)

Para estes números, parece aceitável a aproximação, que, basicamente, é um modelo recursivo, em que a população infectada no momento n depende apenas da população infectada momento n-1, ou seja, x(n)=Rx(n-1). No exemplo da figura, R=1.28.
Numa população finita, nomeadamente num grupo pequeno, o modelo exponencial tem limites, os valores atingidos não podem aproximar-se do total da população.
É aqui que surge o mapa logístico, mencionado noutro local deste blogue, também um modelo recursivo, mas que tenta reflectir a ideia de que a população infectada no momento n é proporcional à população infectada e à população não infectada no momento n-1, ou seja, x(n)=Rx(n-1)[N-x(n-1)].
Sem perda de generalidade, costuma considerar-se a população total ser 1 e x ser a fracção da população, e não o seu valor absoluto. Nesta figura, uma simulação com x(0)=0.0002 e R=1.28:

A população infectada cresceria muito rapidamente, abrandando para atingir o seu máximo em menos de 40 dias. Mas seriam catastróficos os valores atingidos.

Um modelo tem de ser mais elaborado, não se pode ficar pelo ponto de equilíbrio correspondente à exaustão da população. É necessário entrar em linha de conta com a percentagem de infectados que se tornam imunes, com o tempo de incubação, com a distribuição não uniforme da população, etc.

Curiosamente, estes modelos não andam muito longe dos modelos de influência, de contágio, de propagação de ideias nas redes sociais, desde a política à moda.

A revisitar noutro momento.

O mapa logístico

O mapa logístico é a equação recursiva
     x(n) = rx(n-1)[1-x(n-1)]
com r no intervalo [0, 4] e condição inicial x(0) entre 0 e 1, e costuma ser usado para modelizar crescimentos exponenciais em que se considera a condição de a população ser finita.

A população total é 1 e r representa a taxa de crescimento. Neste exemplo, fizemos x(0) = 0.001 e r=1.04, isto é, um milésimo da população afectada e taxa de crescimento 4%.

Uma propriedade desta equação é que, para r no intervalo [1, 2], a população tende para (r-1)/r, independentemente do valor inicial x(0). Neste caso, aproximadamente 0.04.

Para outros valores de r, nomeadamente no intervalo [3,4], esta equação assume um comportamento caótico. Veja-se o caso em que r=3.6

Há muitas situações que podem ser modelizadas pelo mapa logístico, sempre que se misture quem escolhe de acordo com a maioria e quem escolhe de acordo com a minoria: eu escolho um curso porque muitos escolhem e eu não escolho um curso porque muitos escolhem, eu vou pelo caminho A porque a maioria vai e eu não vou pelo caminho A porque a maioria vai, etc.

Estes comportamentos são potencialmente geradores de situações caóticas.
Esta figura muito conhecida mostra o valor para que tende x(n) em função do valor de r

e revela aquele ponto de bifurcação a partir do qual o sistema se torna caótico. Ver, por exemplo, aqui.

Placard

Estou a escrever uns minutos antes do Braga - Sporting, da Taça de Liga.
Lembrei-me - acho que pela primeira vez - de ir ver as apostas 1X2 no Placard, que estão em 1.97x, 3.70x e 3.70x, para a vitória do Braga, empate e vitória do Sporting, respectivamente.
Como é obvio, não há maneira garantida de ganhar num jogo destes.
Podemos distribuir o prejuízo, apostando por exemplo 100/1.97 no 1, 100/3.70 no X e também 100/3.70 no 2, e assim, qualquer que seja o resultado, ganhamos 100€.
Mas quanto é que teríamos de gastar para isso? 100/1.97 + 100/3.70 + 100/3.70 = 104.82€, mais do que os 100€, como seria de esperar. Estes 4.82€ seriam o lucro da organização...
Para ganhar, é preciso arriscar, como em tudo na vida...
O Placard não é um jogo de sorte pura, os conhecimentos futebolísticos do apostador têm uma palavra a dizer, o jogador pode apostar em acreditar mais ou menos num determinado resultado do que a média dos apostadores.
Vi agora que o Guimarães - Porto, de amanhã, paga 4.25x, 3.70x e 1.72x.
Se eu estivesse confiante em que o Guimarães não ganharia, poderia apostar 100/3.70 = 27.02€ no X e 100/1.72 = 58.14€ no 2, gastando 85.16€ e ganhando 100€ se um destes dois resultados se verificasse.
Claro que perderia os 85.16€ se o Guimarães ganhasse...